Gaussian Processes Explained: A Visual Introduction

Gaussian Processes (GPs) are among the most elegant and powerful tools in machine learning and statistics. They provide a principled, probabilistic approach to regression and classification that naturally handles uncertainty quantification.

What are Gaussian Processes?

A Gaussian Process is a collection of random variables, any finite number of which have a joint Gaussian distribution. In the context of machine learning, we use GPs to define distributions over functions.

Mathematical Foundation

Formally, a Gaussian Process is completely specified by its mean function $m(x)$ and covariance function $k(x, x')$:

$f(x) \sim \mathcal{GP}(m(x), k(x, x'))$

Where:

• $m(x) = \mathbb{E}[f(x)]$ is the mean function
• $k(x, x') = \mathbb{E}[(f(x) - m(x))(f(x') - m(x'))]$ is the covariance function

Example :

Example of Matrix rendering:

Test Latex code for the Simpson method:

Matrix Notation

For a finite set of input points $\mathbf{X} = \{x_1, x_2, \ldots, x_n\}$, we can represent the Gaussian Process in matrix form:

$\mathbf{f} \sim \mathcal{N}(\boldsymbol{\mu}, \mathbf{K})$

Where:

• $\mathbf{f} = [f(x_1), f(x_2), \ldots, f(x_n)]^T$ is the vector of function values
• $\boldsymbol{\mu} = [m(x_1), m(x_2), \ldots, m(x_n)]^T$ is the mean vector
• $\mathbf{K}$ is the $n \times n$ covariance matrix with entries $K_{ij} = k(x_i, x_j)$

The covariance matrix has the form:

For predictions at test points $\mathbf{X}_* = \{x_{*1}, x_{*2}, \ldots, x_{*m}\}$, the joint distribution is:

Where:

• $\mathbf{K}_*$ is the $n \times m$ cross-covariance matrix between training and test points
• $\mathbf{K}_{**}$ is the $m \times m$ covariance matrix of test points

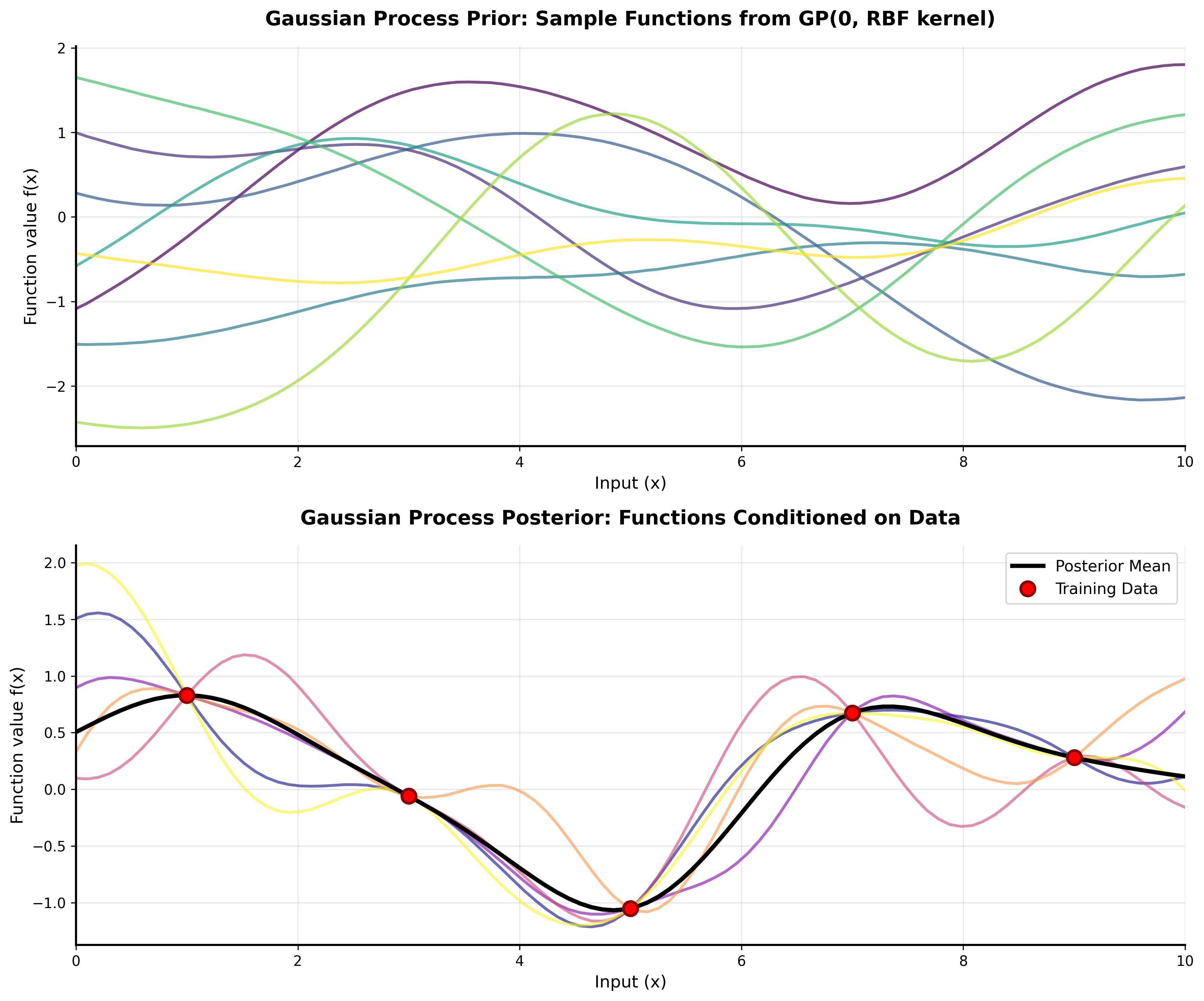
Figure 1: A Gaussian Process with RBF kernel showing the mean prediction (blue line) and uncertainty bands (shaded area). The red dots represent training data points.

Key Properties

1. Flexible non-parametric model: GPs don't assume a fixed functional form
2. Uncertainty quantification: They provide error bars on predictions
3. Kernel-based: The choice of kernel determines the properties of functions we're modeling

Common Kernels

The choice of kernel function is crucial as it encodes our assumptions about the function we're modeling. Here are some popular kernels:

Figure 2: Comparison of common GP kernels showing their covariance functions.

RBF (Radial Basis Function) Kernel

import numpy as np

def rbf_kernel(x1, x2, length_scale=1.0, variance=1.0):
    """
    RBF kernel function
    """
    sqdist = np.sum(x1**2, 1).reshape(-1, 1) + np.sum(x2**2, 1) - 2 * np.dot(x1, x2.T)
    return variance * np.exp(-0.5 / length_scale**2 * sqdist)

Matérn Kernel

The Matérn kernel is a generalization of the RBF kernel and is particularly useful for modeling functions that are not infinitely differentiable.

Implementation Example

Here's a simple implementation of Gaussian Process regression:

import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import solve_triangular, cholesky
from scipy.optimize import minimize

class GaussianProcessRegressor:
    def __init__(self, kernel, noise_variance=1e-6):
        self.kernel = kernel
        self.noise_variance = noise_variance
        
    def fit(self, X, y):
        self.X_train = X
        self.y_train = y
        
        # Compute kernel matrix
        K = self.kernel(X, X)
        K += self.noise_variance * np.eye(len(X))
        
        # Cholesky decomposition for numerical stability
        self.L = cholesky(K, lower=True)
        self.alpha = solve_triangular(self.L, y, lower=True)
        
    def predict(self, X_test, return_std=False):
        K_star = self.kernel(self.X_train, X_test)
        mu = K_star.T @ solve_triangular(self.L, self.alpha, lower=True)
        
        if return_std:
            K_star_star = self.kernel(X_test, X_test)
            v = solve_triangular(self.L, K_star, lower=True)
            var = np.diag(K_star_star) - np.sum(v**2, axis=0)
            return mu, np.sqrt(var)
        
        return mu

# Example usage
X_train = np.array([[1], [3], [5], [6], [7], [8]])
y_train = np.array([1, 3, 5, 6, 7, 8]) + 0.1 * np.random.randn(6)

# Create and fit the model
gp = GaussianProcessRegressor(lambda x1, x2: rbf_kernel(x1, x2, length_scale=1.0))
gp.fit(X_train, y_train)

# Make predictions
X_test = np.linspace(0, 10, 100).reshape(-1, 1)
mu, std = gp.predict(X_test, return_std=True)

# Plot results
plt.figure(figsize=(10, 6))
plt.plot(X_train, y_train, 'ro', label='Training data')
plt.plot(X_test, mu, 'b-', label='Mean prediction')
plt.fill_between(X_test.ravel(), mu - 2*std, mu + 2*std, alpha=0.3, label='95% confidence')
plt.legend()
plt.title('Gaussian Process Regression')
plt.show()

Applications

Gaussian Processes are particularly useful in:

1. Bayesian Optimization: Finding global optima of expensive black-box functions
2. Time Series Modeling: Capturing temporal dependencies with appropriate kernels
3. Spatial Statistics: Kriging and geostatistics
4. Active Learning: Selecting informative data points based on uncertainty

Advantages and Limitations

Advantages

• Probabilistic predictions with uncertainty quantification
• No need to specify functional form a priori
• Works well with small datasets
• Principled hyperparameter learning via marginal likelihood

Limitations

• Computational complexity O(n³) for training
• Memory requirements O(n²)
• Choice of kernel can be challenging
• May struggle with high-dimensional inputs

Conclusion

Gaussian Processes provide a powerful and elegant framework for regression and classification. Their ability to quantify uncertainty makes them particularly valuable in scientific applications and decision-making under uncertainty.

The key to successful GP modeling lies in choosing appropriate kernels and properly handling computational considerations for larger datasets through techniques like sparse GPs or inducing points.

Want to learn more? Check out my other posts on Bayesian Methods and Mathematical Foundations.